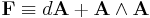BF model

The BF model is a topological field theory, which when quantized, becomes a topological quantum field theory. BF stands for background field. B and F, as can be seen below, are also the variables appearing in the Lagrangian of the theory, which is helpful as a mnemonic device.

We have a 4-dimensional differentiable manifold M, a gauge group G, which has as "dynamical" fields a two-form B taking values in the adjoint representation of G, and a connection form A for G.

The action is given by

$S=\int_M K[\mathbf{B}\wedge \mathbf{F}]$

where K is an invariant nondegenerate bilinear form over $\mathfrak{g}$ (if G is semisimple, the Killing form will do) and F is the curvature form

$\mathbf{F}\equiv d\mathbf{A}%2B\mathbf{A}\wedge \mathbf{A}$

This action is diffeomorphically invariant and gauge invariant. Its Euler-Lagrange equations are

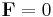$\mathbf{F}=0$ (no curvature)

and

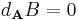$d_\mathbf{A}B=0$ (the covariant exterior derivative of B is zero).

In fact, it is always possible to gauge away any local degrees of freedom, which is why it is called a topological field theory.

However, if M is topologically nontrivial, A and B can have nontrivial solutions globally.

External links

http://math.ucr.edu/home/baez/qg-fall2000/qg2.2.html

BF model

See also

External links